DOI：10.1016/J.CMA.2024.116826

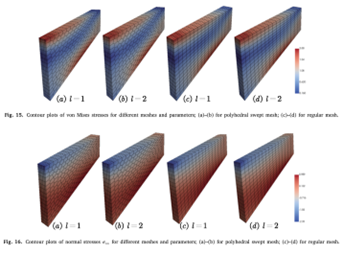
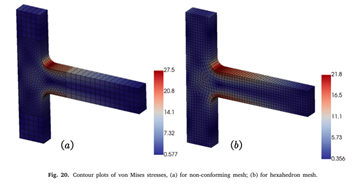
Abstract：We present a first-order stabilization-free virtual element method (VEM)for three-dimensional linear elastic problems in this paper. VEM has been increas-ingly used in various fields of engineering, but the need of stabilization yields amethod that cannot be used without care, e.g. in nonlinear engineering applications.In this work, by increasing the order of the strain model, a new virtual element for-mulation is constructed for three-dimensional problems that does not require anystabilization term. The core concept involves adapting the virtual element space toenable the computation of a higher-order Lz projection operator, guaranteeing anaccurate representation of the element energy in terms of strain and stress. Thiswork describes the calculation process of the original H, projection operator andthe higher-order L2 projection operator for three-dimensional problems. Eigenvalueanalysis allows to derive an approximate relation between the polynomial order andthe number of element vertices. Some benchmark problems illustrate the capabilityof the stabilization-free VEM for three-dimensional linear elastic problems.