DOI： 10.1016/j.cma.2024.117683

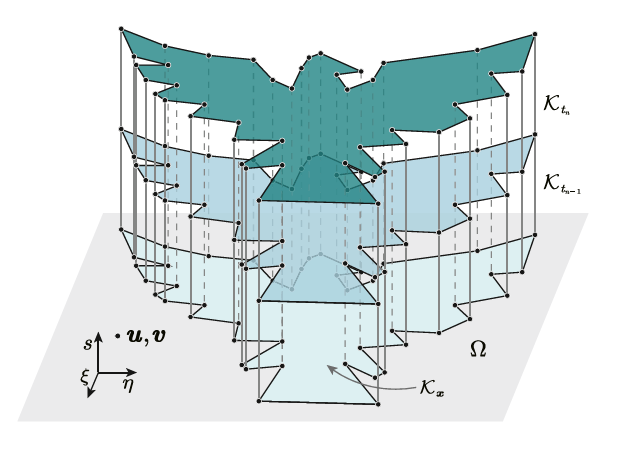
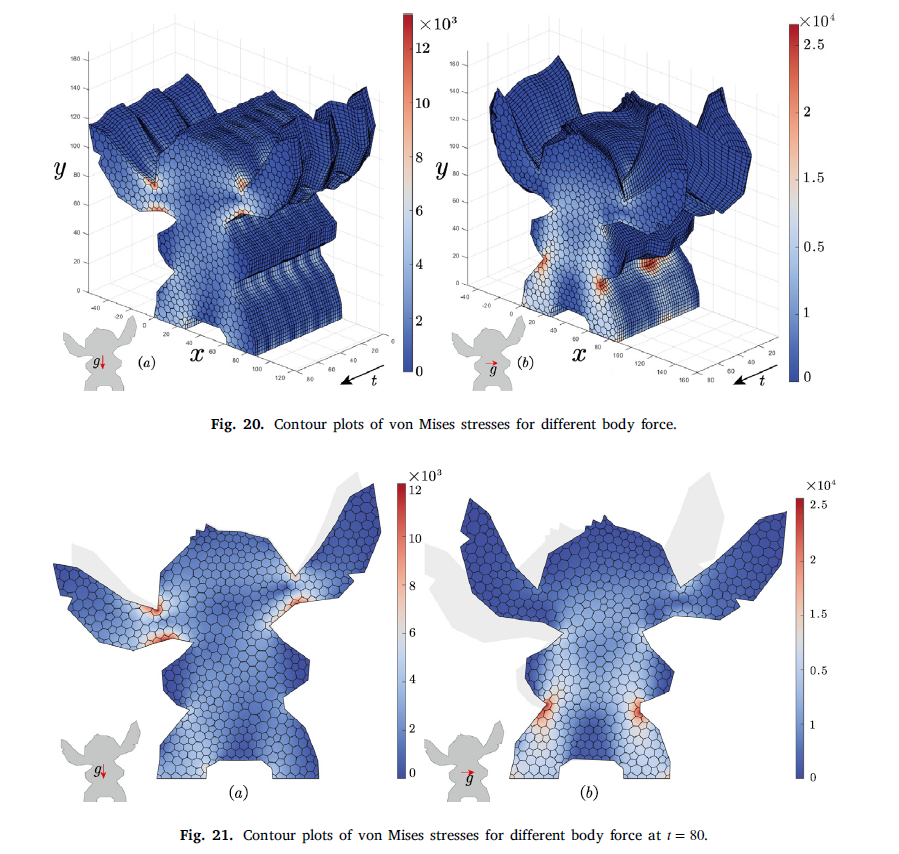
Abstract： In this work, a space-time virtual element method is presented for the discretization of the two-dimensional elastodynamics in a space-time cylinder. The basic idea of the space-time scheme is to treat time as an additional dimension. This approach has been extensively applied to numerous initial value problems based on the finite element method and virtual element method. However, there has been no report on the application of the space-time virtual element method in elastodynamics. The variational formulation and space-time bilinear format are derived based on Hamilton’s principle to achieve this. The discretization space is obtained by the virtual element method in space and the upwind finite element method in time. The space-time mesh is obtained as a tensor product of space and time meshes, then the element stiffness matrix for the elastodynamic problem can be obtained based on the Kronecker product directly. Some two-dimensional examples solved by the developed spacetime virtual element method are given to demonstrate the accuracy and stabilization. MATLAB codes for the space-time virtual element and finite element methods can be downloaded from https://github.com/Qinxiaoye/VEM-spcae-time-dynamic.