DOI： 10.1016/j.cma.2024.117258

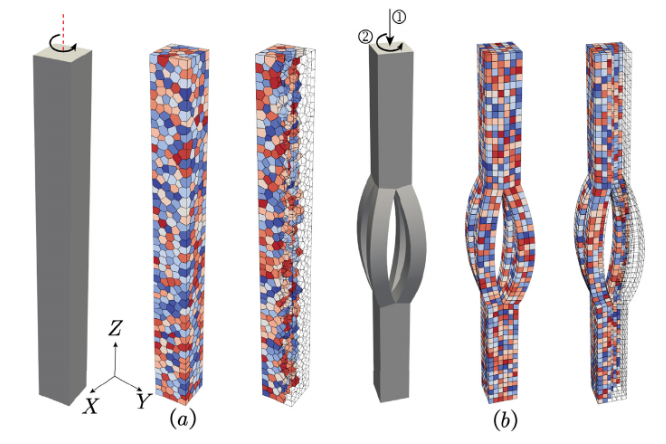
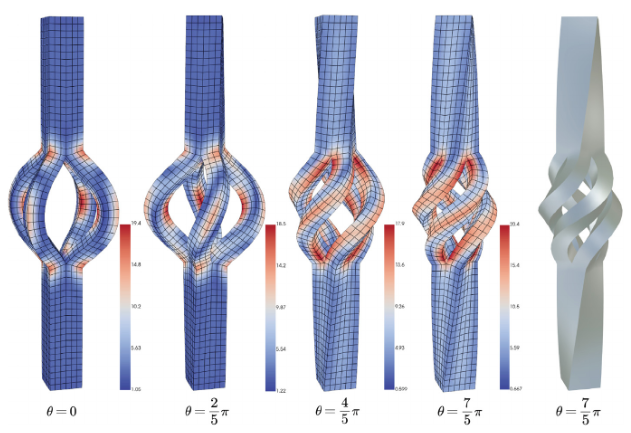
Abstract： In this work, we develop a general high-order virtual element method for three-dimensional linear and nonlinear elastic problems. Applications of the virtual element method (VEM) in three-dimensional mechanics include linear elasticity problems, finite elastic strain problems, finite deformation plasticity problems, etc. But besides linear elastic problems, see e.g. Visinoni, 2024, the numerical schemes were all based on a first-order approximation of the displacement. We derive three-dimensional elastic problems, including linear elastic problems and for the first time hyperelastic problems. Similar to previous work, we discuss the calculation method of three-dimensional high-order projection operators of vector fields and calculate the tangent stiffness matrix of elastic problems according to the variational scheme. Since traditional VEM requires the use of stabilization terms to ensure the correctness of the rank of the stiffness matrix, we give suggestions for the selection of stabilization terms for high-order virtual element methods in both linear and nonlinear elasticity. Finally, we illustrate the accuracy, convergence, and stability of the high-order VEM for elastic problems by means of some classic elastic and hyperelastic examples. In addition, we also apply the developed methodology to some complex and difficult problems which illustrate the adaptability of the method to engineering problems.